In his book – Value Investing: From Graham to Buffett and Beyond, Bruce Greenwald discusses how to value growth using the ‘Growth Value Matrix’. Here’s an excerpt from the book:
In general, the value created by growth depends on two factors. The first is the profitability of the incremental capital employed; the greater the amount by which incremental returns exceed the cost of capital, the greater will be the value created by each dollar invested. So our first variable is expressed as a ratio, ROC/R.
The second factor is the amount of capital that can be employed to earn these franchise returns. That depends on how fast the franchise grows. The limits of sustainable growth are some fraction of the cost of capital. As we said, if growth equaled the cost of capital for any lengthy period, the return on capital would be infinite. We know that isn’t possible, so we have to accept the fact that G/R will be less than one. We use 25 percent, 50 percent, and 75 percent as three standardized percentages.
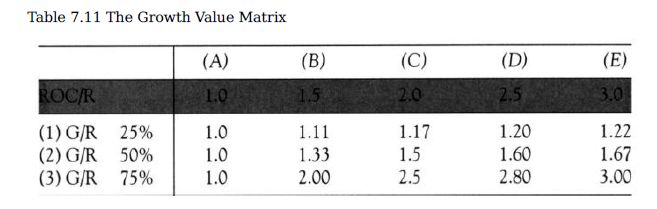
Based on more algebra, which we have consigned to the appendix, we offer Table 7.11 to represent the relationship between the value of a business growing within a franchise and the value of the same business without growth, or PV/EPV.
The number within each cell is the PV/EPV ratio for the appropriate values of ROC/R and G/R. In Column A, where the return on capital is the same as the cost of capital (ROC/R = 1), growth adds nothing to EPV; the ratio of PV/EPV remains 1. But as we move to Column B, where ROC/R = 1.5, growth starts to matter. If the growth rate is 25 percent of the cost of capital, then PV/EPV = 1.11.
To flesh this out, if the return on incremental capital is 12 percent and the cost of capital is 8 percent, a business that grows 2 percent a year is worth 11 percent more than one with no growth. If it grows 4 percent a year, it is worth 33 percent more; if it grows at 6 percent, the value is twice that of its no-growth twin. At the extreme, a business with an incremental return of 24 percent, a cost of capital of 8 percent, and growth of 6 percent a year is worth three times as much as the business without growth.
The striking feature of Table 7.11 is how small the growth multiples are. It takes high returns on capital combined with high growth rates to move the multiple above 2. If a company without growth sells at a price to earnings ratio (P/E) of 16 (i.e., the EPV = 16 x the earnings), which is common today, then a company with a P/E of 48 (i.e., 3 x the EPV) ought to have a return on capital three times the cost of capital, and a growth rate of 75 percent of that cost. With a cost of capital of 12 percent, that would mean a ROC of 36 percent and a growth rate of 9 percent, not for the next year or two but for a long time into the future.
For all the latest news and podcasts, join our free newsletter here.
Don’t forget to check out our FREE Large Cap 1000 – Stock Screener, here at The Acquirer’s Multiple: